Stability Analysis¶

The stability of a biochemical system is determined by the eigenvalues of the Jacobian matrix. Given 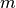$m$ floating species and 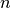$n$ reactions, the Jacobian matrix is defined as follows:

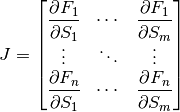
$J=\begin{bmatrix} \dfrac{\partial F_1}{\partial S_1} & \cdots & \dfrac{\partial F_1}{\partial S_m} \\ \vdots & \ddots & \vdots \\ \dfrac{\partial F_n}{\partial S_1} & \cdots & \dfrac{\partial F_n}{\partial S_m} \end{bmatrix}$

where 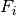$F_i$ is the ith differential equation and 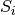$S_i$ the ith floating species. From roadRunner it is easy to obtain the Jacobian matrix using the command:

Jac = rr.getFullJacobian()

which returns the Jacobian matrix in the variable Jac.

It is possible for full Jacobian to be singular. In these situations one should call instead the related method, getReducedJacobian().

Previous topic

Metabolic Control Analysis

Next topic

Accessing the SBML Model Variables

This Page