Stoichiometric Analysis¶
Preliminaries¶
A network of 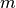 chemical species and
chemical species and 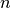 reactions can be described by the
reactions can be described by the
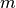 by
by 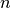 stochiometry matrix
stochiometry matrix 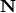 .
. 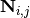 is the net number of
species
is the net number of
species 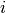 produced or consumed in reaction
produced or consumed in reaction 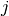 . The dynamics of the network are
described by
. The dynamics of the network are
described by

where  is the vector of species concentrations,
is the vector of species concentrations, 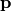 is a vector of time independent parameters, and
is a vector of time independent parameters, and 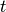 is time.
is time.
Each structural conservation, or interchangably, conserved sum (e.g. conserved moiety) in
the network coresponds to a lineraly dependent row in the stoichiometry matrix 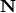 .
.
If there are conserved sums, then the row rank,  of
of 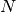 is
is 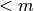 , and
the stochiometry matrix
, and
the stochiometry matrix 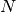 may first be re-ordered such that the first
may first be re-ordered such that the first  are linearly
independent, and the remaining
are linearly
independent, and the remaining 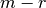 rows are linear combinations of the first
rows are linear combinations of the first  rows. The reduced stochiometry matrix
rows. The reduced stochiometry matrix 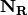 is then formed from the first
is then formed from the first
 rows of
rows of 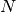 . Finally,
. Finally, 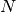 may be expressed as a product of the
may be expressed as a product of the 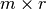 link matrix
link matrix 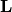 and the
and the 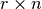
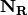 matrix:
matrix:
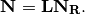
The link matrix 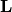 has the form
has the form
![\mathbf{L} = \left[ \begin{array}{c}
\mathbf{I}_{r} \\
\mathbf{L}_0 \end{array} \right],](_images/math/46e1e32b694095fdaf03b9ca61de351f61747fa1.png)
where 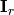 is the
is the 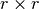 identity matrix and
identity matrix and 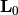 is a
is a 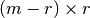 matrix.
matrix.
Methods¶
The following methods are related to the analysis of the stoichiometric matrix.
| ExecutableModel.getStoichiometryMatrix() | Returns the current stoichiomentry matrix, a 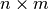 matrix where matrix where 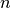 is the number of species which take place in reactions (floating species) and is the number of species which take place in reactions (floating species) and 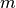 is the number of reactions. is the number of reactions. |
| RoadRunner.getLinkMatrix() | Returns the full link matrix, L for the current model. The Link matrix is an m by r matrix where m |
| RoadRunner.getNrMatrix() | Returns the reduced stoichiometry matrix, 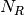 , which wil have only r rows where r is the rank of , which wil have only r rows where r is the rank of |
| RoadRunner.getConservationMatrix() | Returns a conservation matrix 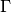 which is a which is a 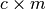 matrix matrix |
| RoadRunner.getL0Matrix() | Returns the L0 matrix for the current model. The L0 matrix is an (m-r) by r matrix that expresses |
| ExecutableModel.getNumConservedMoieties() | Returns the number of conserved moieties in the model. |
| ExecutableModel.getConservedMoietyIds([index]) | Returns a vector of conserved moiety identifier symbols. |
| ExecutableModel.getConservedMoietyValues([index]) | Returns a vector of conserved moiety volumes. |
| ExecutableModel.setConservedMoietyValues(...) | Sets a vector of conserved moiety values. |